独学で学ぶFP2級｜相続・事業承継（３）
tadanori
Aruの雑記（Aruaru0）
独学で学ぶFP2級｜金融資産運用編（５）
tadanori
記事内に商品プロモーションを含む場合があります
FP2級の学習（独学）に役立つ無料テキスト（教科書）を作成しました。このテキストはFP2級試験の幅広い範囲を網羅しており、効果的な学習の参考資料として活用できます。ぜひ、FP２級合格のために役立ててください。また、記事には、独自の試験対策コメントも入れていますので参考にしてください。
CFPが作成！FP2級の無料Webテキスト（2024）〜「独学で学ぶFP２級：目次」
FP2級試験範囲を順に進めていきます。この記事では以下を取り上げます。
金融資産運用
- 金融派生商品
- ポートフォリオ運用
Contents
金融派生商品
金融派生商品（デリバティブ）とは
金融派生商品とは、株式や債券などの金融商品のリスク回避を目的とした取引のことで、先物取引、オプション取引、スワップ取引などがある
先物取引
先物取引とは
特定の金融商品を、将来の特定の期日を受渡日として、あらかじめ決めた価格で売買することを約束する取引
先物取引のポイント
- 期日前でも、反対売買で取引を終了させることが可能
- 決済方法は、差金決済（売買差額のみの決済）と現物決済がある
- 少額の証拠金で多額の取引ができるので、レバレッジ効果がある
- 先物を買うことを買い立て、売ることを売り立てと呼ぶ
取引手法
ヘッジ取引
現物と反対のポジションを組むことにより価格変動を回避（ヘッジ）する取引。保有している現物の値下がりリスクをヘッジするための「売りヘッジ」と、現物の値上がりリスクを回避するための「買いヘッジ」がある
裁定取引（アービトラージ）
割安な投資対象を買い、割高な投資対象を売るポジションを取ることで、両者のサヤ（価格差）を抜こうとする手法
スペキュレーション取引
相場が上がると思えば買い、相場が下がると思えば売り、反対売買で利益をえる手法。スペキュレーションとは投機の意味。株価の変動を利用して、短期的な売買を主体に利益を得ようとする取引
オプション取引
オプション取引とは
オプション取引とは、対象となる商品（原資産）を、一定の期日までにあらかじめ決めた価格で買う権利もしくは売る権利の売買を行うこと。
- あらかじめ決めた価格を権利行使価格という
- 買う権利をコールオプション、売る権利をプットオプションと呼ぶ
- 権利の値段のことをプレミアム（オプション料）という
- 権利を行使しないことも可能
- 取引所取引と店頭取引がある
試験対策としては、先物取引と同じに感じるかもしれませんが、こちらは売る権利・買う権利という、権利を売買している部分が違います
取引手法
オプション取引の基本的な取引は以下の４つになる
| コール・オプション （買う権利） | プットオプション （売る権利） | |
| 買手 | コール・オプション買い ※値上がりすると利益 | プット・オプション買い ※値下がりすると利益 |
| 売手 | コール・オプション売り ※値上がりすると損失 | プット・オプション売り ※値下がりすると損失 |
オプション取引の利益
オプション取引の利益と損失の関係は以下のようになる
| 利益 | 損失 | |
| 買手 | 無限大 | プレミアム |
| 売手 | プレミアムが最大 | 無限大 |
下図は、コールの買い・売り、プットの買い・売りの原資産の価格変化と利益と損失をグラフにしたもの。図からわかるように買手の損失はプレミアムに限定され、売手はプレミアムの利益が最大となる。
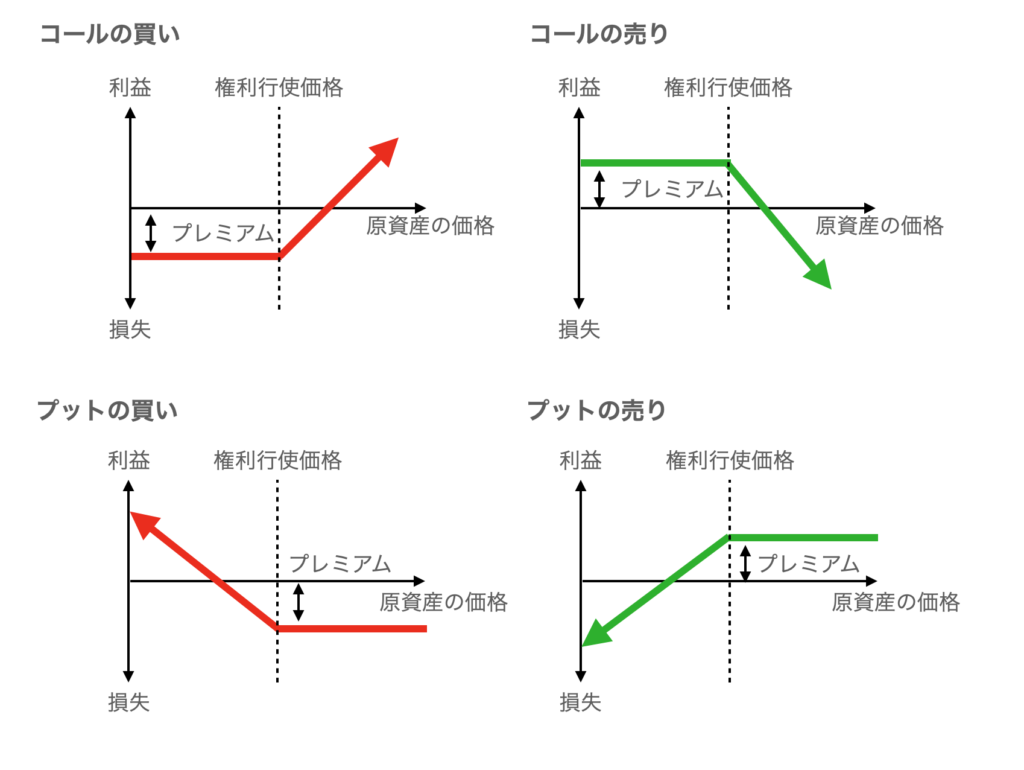
試験対策としては、コール（買い）とプット（売り）の意味と、買う側と売る側がいつ利益が出るかを理解しておきましょう。
上のオプション取引のように、グラフでイメージとして理解した方が簡単かもしれません。
補足説明
コールの買いと、コールの売りについて少し補足説明をしておきます。
買う権利とは、特定の価格で購入する権利のことです。
資産は買わなくても良いのでを買った側は、権利を得るためのオプション料を払っても、資産を購入する義務はありません
なので、資産が下がった場合は購入しないことができます。ですから、オプション料が損失の最大になります。
逆に、上がった場合は上がった額からオプション料を引いた額が利益になります（グラフ参照）。
一方、コールオプションを売った側は、オプション料が手に入ります。
しかしながら、価格が上昇した場合は設定した（低い金額で）売らなければならないので、上がった分だけ損失がでます
スワップ取引
スワップ取引は、金融機関同士が互いに将来発生する金利債務などのキャッシュフローを交換する取引のこと。スワップ取引として代表的なものに金利スワップと通貨スワップがある
金利スワップ
同じ通貨で異なるタイプの金利を交換するスワップ。典型的な金利スワップとしては変動金利と固定金利を交換するものがある
通貨スワップ
異なる通貨で利息や元本を交換するスワップ
スワップ取引がなぜ成立するのか理解が難しいです。「Aさんは将来金利が下がるの変動金利にしたい」、一方「Bさんは将来金利は上がるので固定金利にしたい」など、お互いに将来への予想が違うのでスワップが成り立つと考えたらわかりやすいかもしれません
外国為替証拠金取引（FX）
外国為替証拠金取引は、証拠金を差し入れて２つの国の通貨（日本円と米ドルなど）の為替相場を予測して売買を行う取引。法令により証拠金倍率は最大25倍に制限されている
FX取引は、少額の証拠金で、その何倍もの売買ができるレバレッジ効果があります。
FXはデリバティブ取引の一種です
ポートフォリオ運用
ポートフォリオとは
ポートフォリオ（Portfolio）とは、金融商品の組み合わせのこと。「ポートフォリオを組む」とは、どのような金融商品をどの程度の割合で持つかを検討するという意味になる
ポートフォリオ運用を行うことで、分散投資によるリスク低減効果が期待できる
ポートフォリオについてより詳しく知りたい方はこちら
ポートフォリオに関する記事です。理解を深める助けになると思います。
ポートフォリオの資産配分の決め方｜myINDEXを使った方法を解説
資産配分ツールで自分のポートフォリオを作成しよう。myINDEX活用術
ポートフォリオ運用の基礎
効率的市場仮説
ポートフォリオ運用では、市場が効率的であるということ（効率的市場仮説）を前提としている
効率的市場仮説とは、「市場参加者が合理的な行動をとり、すべての情報も完全に市場価格に即座に織り込まれるため、継続して市場平均よりも高い運用成果を得ることはできない」という仮説のこと
効率的市場仮説に基けば、現在利用可能は情報は即座に価格に反映されるため、将来の価格変動は予測できないことになる。また、長期で見ると市場平均以上の収益は見込めないことになる
簡単に言えば、市場に参加している人は、市場参加者はプロが多く知識もあるので、そこで決まった価格は常に適正価だという考え方です
アセットアロケーション
アセット（Asset）は資産、アロケーション（Allocation）は、割り当て、配分といった意味の英語で、アセットアロケーションとは、運用する資産の配分を決めることをいう。組み入れる資産としては、国内/海外の株式/債券/不動産、現金、金などがある。
アセットアロケーションの目的は、資産の分散によりリスクを軽減し、安定した運用成果を上げること。
資産クラスと比率を決めると、過去の実績ベースの収益期待率とリスクが計算できるので、それを参考に自身の投資目標に合わせた資産配分を行う
例えば、日本国債：日本株：米国債：米国株を20:20:20:40の割合で配分すると以下のようになる。2003年7月末〜2023年7月末の20年間の過去の実績データ（円ベース）では、このポートフォリオの期待収益率は約7%、リスクは約11%となる。
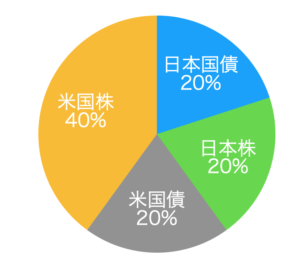
積立投資などでも、アセットアロケーションという考え方は大切になっています。
期待収益率とリスク（標準偏差）
期待収益率
特定の資産について、運用に得ることができると予想される平均的な収益率。将来を予測するのは難しいので過去実績などから計算することが多い
リスク（標準偏差）
期待収益率のばらつきの大きさをリスクといい、統計学で使われる「分散」や「標準偏差」で表す。この尺度が大きいほどリスクが高いことになる
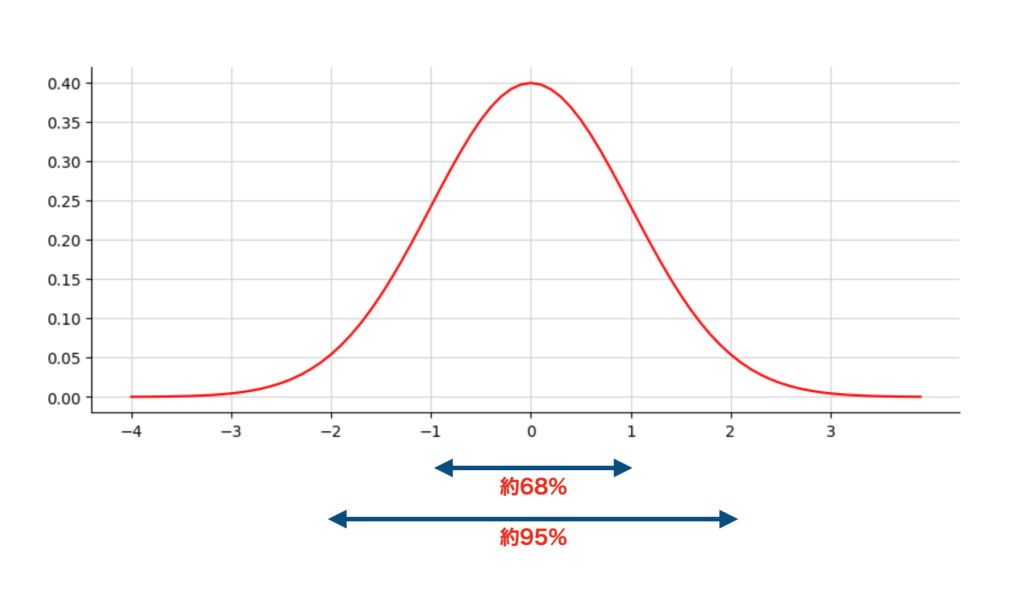
標準偏差を$\sigma$としたとき、正規分布の場合は$\pm 1\sigma$に68%、$\pm 2\sigma$に95%が入るとされている。
これを使って、期待収益率が7%、リスクが11%のポートフォリオは、68%の確率で-4%~18%の範囲に、95%の確率で-15%~29%の範囲に収まると考えることができる
ポートフォリオの評価
ポートフォリオの期待収益率
ポートフォリオの期待収益率は、組み入れた資産の加重平均となります
| 資産 | 組み入れ比率 | 期待収益率 |
| 資産A | 40% | 10% |
| 資産B | 30% | 5% |
| 資産C | 30% | 1% |
$\begin{eqnarray}
期待収益率&=&\frac{40}{100}\times 10\% + \frac{30}{100}\times 5\% + \frac{30}{100}\times 1\%=5.8\%
\end{eqnarray}$
ポートフォリオのリスク
ポートフォリオのリスク（標準偏差）を求めるには、期待収益率、予想収益率、生起確率の３つが必要になる
例えば、以下のような予想収益率と生起確率とする
| 生起確率 | 予想収益率 | |
| 好況 | 30% | 15% |
| 普通 | 50% | 5% |
| 不況 | 20% | -10% |
期待収益率＝0.3×15% + 0.5×5% + 0.2×(-10%) = 5%
分散は期待収益率の5%を使って以下のように計算する
分散＝0.3×(15%-5%)2 + 0.5×(5%-5%)2 + 0.2×(-10%-5%)2 =75
偏差＝$\sqrt{分散} =\sqrt{75} \simeq 8.66$%
分散の計算に(予想収益率ー期待収益率)2と２乗が入っていることに注意してください。また、分散を出してから偏差を計算するステップにも注意です。
各商品の相関係数
相関係数とは、２つの資産の関連性の強さを示すもの。$-1\sim1$の範囲の値をとり、1に近いほど関連性（片方が上がれば、もう一方も上がる）が強く、-1に近いほど逆方向への関連性（片方が上がれば、もう一方は下がる）
| 正の相関（相関係数＞０） | ２つの資産は、同じ動きをする。相関係数が１の場合は全く同じ動きをすることを示す |
| 無相関（相関係数＝０） | ２つの資産に全く関係性がない |
| 負の相関（相関係数＜０） | ２つの資産は、反対の動きをする。相関係数が−１の場合は、完全に逆の動きになることを示す |
試験対策としては、期待収益率、リスク（偏差）、相関係数の意味はちゃんと理解するようにしましょう
y = 2xの関係となる（資産yは、資産xの2倍の値動きをする）場合も、相関係数は１となります。このあたりは試験には出ないと思いますが、数学的に理解しておくポイントです。（相関係数＝１は、片方が１円上がれば他方も１円上がるという意味じゃないです）
シャープレシオ
ポートフォリオの収益率から無リスク資産の収益率を引いて、ポートフォリオの収益率の標準偏差（＝リスク）で割った値をシャープレシオと呼ぶ
リスクをとるからには無リスク資産より収益率が高くなければなりません
シャープレシオでは、収益率をリスクで割ることで、リスク１に対するリターンを計算する
値がリスク１単位あたりの数字になるので、異なる収益率とリスクの資産のリターンを比較することができるようになる点がポイントとなる
$$
シャープレシオ=\frac{ポートフォリオの収益率 – 無リスク資産の収益率}{ポートフォリオの収益率の標準偏差}
$$
シャープレシオを使えば、資産A（期待収益率5%, リスク10%）と資産B（期待収益率4%, リスク9%）のどちらが効率が良いかを評価することができます
現在価値（PV）
現在価値（PV）とは、将来獲得するお金の現在価値を示すもの。
具体的には、「X年後の100万円は、現在いくらの価値か？」ということを計算したもの
考え方としては、「現在のお金を利率r％で運用したらX年後にいくらになるか？」を逆に計算する。PVの場合、利率を割引率という
$$
PV = \frac{将来受け取る金額}{(1+割引率)^{n年}}$$
年利1％で考えると、1年後の101万円は、現在の100万円の価値（1年後には利子が1万円つくので）となります
その他
ドルコスト平均法
投資信託などを定期的に同額づつ購入する投資手法。例えば、日経平均に連動するインデックスファンドを毎月1万円購入するのであれば、株価が上昇しているときには少ない口数、株価が下落しているときには多い口数を購入していることになる。
このように、一定額ずつ購入することで安い時は多く買い、高いときには少なく買うということを自動的に行う投資手法をドルコスト平均法と呼ぶ
システマティックリスク（市場リスク）とアンシステマティックリスク（非市場リスク）
システマティックリスク（市場リスク）
市場全体の要因によるリスクのこと。ポートフォリオ運用では回避できないリスク
アンシステマティックリスク（非市場リスク）
資産（株の場合は銘柄など）の要因によるリスクのこと。ポートフォリオへ組み込む銘柄を増やすことにより影響を小さくすることが可能
次の記事
独学で学ぶFP2級｜金融資産運用編（６）
ABOUT ME
2023年5月に54歳で早期退職。自分の時間ができたのでブログを開設。本職はITエンジニア（専門はデータ分析・機械学習）だが、ファイナンシャル・プランナー（CFP®）資格も保有し活動中。投資歴は20年以上。